Temporal Distance Learning in MATLAB
Windy Grid World
Problem:
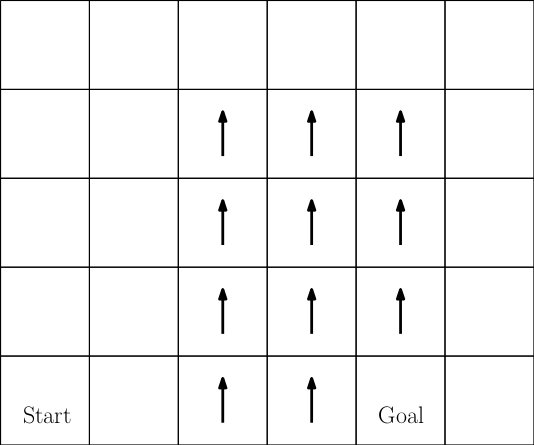
This assignment is to use Reinforcement Learning to solve the following "Windy Grid World" problem illustrated in the above picture. Each cell in the image is a state. There are four actions: move up, down, left, and right. This is a deterministic domain -- each action deterministically moves the agent one cell in the direction indicated. If the agent is on the boundary of the world and executes an action that would move it "off" of the world, it remains on the grid in the same cell from which it executed the action.
Notice that there are arrows drawn in some states in the diagram. These are the "windy" states. In these states, the agent experiences an extra "push" upward. For example, if the agent is in a windy state and executes an action to the left or right, the result of the action is to move left or right (respectively) but also to move one cell upward. As a result, the agent moves diagonally upward to the left or right.
This is an episodic task where each episode lasts no more than 30 time steps. At the beginning of each episode, the agent is placed in the "Start" state. Reward in this domain is zero everywhere except when the agent is in the goal state (labeled "goal" in the diagram). The agent receives a reward of positive ten when it executes any action {\it from} the goal state. The episode ends after 30 time steps or when the agent takes any action after having landed in the goal state.
Solved the problem using Q-learning. Use e-greedy exploration with epsilon=0.1 (the agent takes a random action 10 percent of the time in order to explore.) Use a learning rate of 0.1 and a discount rate of 0.9.
References
[1] github: https://github.com/sinairv/TemporalDifferenceLearning
[2] ebook: http://webdocs.cs.ualberta.ca/~sutton/book/ebook/node65.html
Final Solution
Optimal Solution obtained after convergence as per policy:
